Analisi del rischio e anticorruzione: come valutare al meglio i processi lavorativi?

L’approvazione in Italia della Legge 190/2012 sull’anticorruzione [1] e le indicazioni fornite nel primo Piano Nazionale Anticorruzione (PNA) del 2013 [2] hanno introdotto degli elementi di significativa novità nel contesto della Pubblica Amministrazione (PA) italiana.

Il concetto di corruzione, come definito nella norma del 2012, assume un’accezione ampia, tale da ricomprendere un malfunzionamento dell’Amministrazione a causa dell’uso a fini privati delle funzioni d’ufficio ma anche una devianza dell’azione amministrativa, sia che tali azioni abbiano successo sia nel caso in cui rimangano a livello di tentativo. Con riferimento alla fig.1 possiamo dire che tutti gli aspetti penalistici risultano compresi nella accezione proposta della norma del 2012, con un innovativo ampliamento al concetto di devianza dall’azione amministrativa.

Altri due importanti aspetti innovativi introdotti da questa norma sono il riferimento fornito nel PNA all’adozione di tecniche di risk management e il modello di miglioramento continuo di processo, cardini fondanti nella norma ISO 31000 [3,4] – dedicata ai principi del risk management – che viene assunta come riferimento per le analisi dei processi lavorativi della PA per la prevenzione della corruzione. Questa scelta legata alla gestione del rischio ha imposto dal 2013 ad oggi un enorme sforzo della PA centrale e locale al fine di trasformare l’applicazione della norma sull’anticorruzione da una serie di meri adempimenti formali, spesso infruttuosi, ad uno strumento metodologico di utilità concreta per il controllo reale dell’andamento dei processi lavorativi. Accanto ai concetti del risk management, l’applicazione costante del ciclo di Deming [5], indicato anche come PDCA (Plan Do Check Act, vedi fig.2) e mutuato dalle norme internazionali sul controllo di qualità (famiglia ISO 9000), costituisce la reale sfida di natura culturale/organizzativa che il normatore ha voluto introdurre con la Legge 190/2012 e il PNA per la prevenzione della corruzione.

L’applicazione delle metodologia descritte nella ISO 31000 impongono una continua capacità di pianificazione seguita da una fase realizzativa. Successivamente a queste due fasi, la fase del controllo consente di mettere in evidenza le inevitabili lacune che ogni realizzazione concreta mostra, conducendo ad una fase di identificazione delle migliorie da apportare al riavvio della nuova pianificazione/realizzazione.

Occorre sottolineare ancora come l’introduzione di metodologie a miglioramento continuo legate al modello PDCA per l’anticorruzione in ambito pubblico abbia costituito in questi anni una novità assoluta, che ha obbligato molte strutture pubbliche ad affrontare una sfida stimolante: ripensare e ridisegnare i processi lavorativi che si svolgono al proprio interno, in un’ottica di trasparenza e tracciabilità. Questo esercizio, sebbene finalizzato alla evidenziazione delle situazioni a rischio corruttivo, porta dunque con sé un valido vantaggio collaterale, ossia una potenziale razionalizzazione dei processi in contesti che, in alcuni casi, risultavano cristallizzati nel tempo.

Evidentemente, così come l’analisi del rischio corruttivo è una processo di tipo PDCA, anche lo stesso processo di definizione della metodologia e dei requisiti è soggetto ad un continuo aggiustamento e miglioramento sulla base delle esperienze via via acquisite.

In questo lavoro si concentra l’attenzione sulle metodologie analitiche suggerite nel PNA del 2013 per la valutazione del rischio, evidenziando possibili criticità e miglioramenti auspicabili alla luce di esperienze di applicazione.

Il modello di valutazione del rischio proposto dal PNA

Nell’Allegato 1 del PNA 2013 [2] si definisce l’analisi del rischio come la “valutazione della probabilità che il rischio si realizzi e delle conseguenze che il rischio produce (probabilità e impatto) per giungere alla determinazione del livello di rischio. Il livello di rischio è rappresentato da un valore numerico.”

In termini matematici, il livello di rischio corruttivo R viene definito in [PNA1] come il prodotto

R = P ^. I

avendo indicato con I il livello di impatto (espresso in principio con una scala da 0 a 5) e con P il livello di probabilità (espresso in principio con una scala da 0 a 5 anch’esso).

Ai fini del calcolo del livello di probabilità e di impatto, il PNA propone una serie di indici di valutazione [6]. In particolare, per quanto riguarda la “probabilità” P sono considerate le seguenti sei categorie:

• P₁ – Discrezionalità
• P₂ – Rilevanza esterna
• P₃ – Complessità del processo
• P₄ – Valore economico
• P₅ – Frazionabilità del processo
• P₆ – Controlli.

L’analisi di dettaglio degli indici proposti evidenzia come la probabilità qui espressa non sia intesa unicamente in riferimento al presentarsi della minaccia (cioè la possibilità che si presenti un tentativo di corruttivo per un processo specifico lavorativo) ma anche, e soprattutto, alla quantificazione della probabilità legata allo sfruttamento di vulnerabilità presenti nel processo analizzato, vulnerabilità che possono portare alla realizzazione concreta di una minaccia. Tali indici di valutazione devono essere considerati come delle caratteristiche dei singoli processi e sono riconducibili nella maggior parte dei casi a debolezze intrinseche (ad es. il caso della “Discrezionalità”) e in altri casi a fattori di appetibilità per l’attaccante (ad es. il caso del “Valore economico”). In termini di analisi del rischio, essi rappresentano, quindi, una sintesi di minaccia e vulnerabilità. Va sottolineato che quest’ultimo approccio costituisce un aspetto molto importante dell’impostazione suggerita dal PNA 2013, che sarà oggetto di un prossimo approfondimento dedicato agli indici scelti e alla loro pesatura.

Per quanto riguarda l’impatto, le categorie considerate in [6], su cui sono formulati gli indici di valutazione, sono le seguenti quattro:

• I₁ – Impatto organizzativo
• I₂ – Impatto economico
• I₃ – Impatto reputazionale
• I₄ – Impatto organizzativo, economico e sull’immagine.

Per ognuno degli indici di valutazione di probabilità e impatto, il PNA indica un set di possibili pesi numerici (espressi con dei numeri interi compresi tra 0 e 5). Nella tab.1 che segue sono riportate, a titolo di esempio, le formulazioni e le pesature della “discrezionalità” e dell’”impatto organizzativo”.

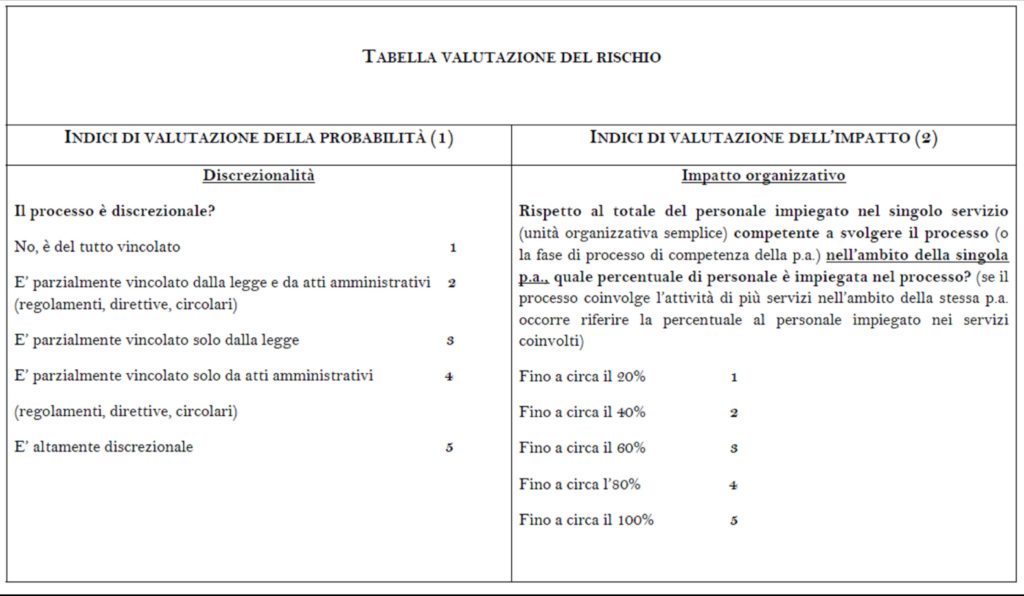
Da questa impostazione deriva che, per ogni singolo processo sotto analisi, si otterrà una serie di valori numerici corrispondenti ai vari indici (in particolare, 6 valori di probabilità e 4 valori di impatto).

Sul modo in cui tali indicatori debbano essere “combinati” per ottenere un valore unico di livello rischio si è espresso nel 2013 il Dipartimento della Funzione Pubblica che in una comunicazione [7] ha chiarito:

1. il valore della “probabilità” va determinato, per ciascun processo, calcolando la media aritmetica dei valori individuati in ciascuna delle righe della colonna “Indici di valutazione della probabilità” dell’allegato 5 al PNA;
2. il valore dell’ “impatto” va determinato, per ciascun processo, calcolando la media aritmetica dei valori individuati in ciascuna delle righe della colonna “Indici di valutazione dell’impatto” al PNA;
3. il livello di rischio R è determinato dal prodotto dei due valori medi della probabilità e dell’impatto e potrà assumere il valore massimo di 25.

Infine, nell’Allegato 1 al PNA 2013 [8] si specifica quanto segue:

“… le indicazioni metodologiche sono raccomandate ma non vincolanti, …”,

volendo suggerire che ogni Amministrazione poteva e può individuare, se ritenuto necessario, modelli più specifici di quello proposto nel 2013, purché adeguati, per la valutazione e gestione del rischio.

Il procedimento proposto in [7] può dunque essere schematizzato, per ogni processo, come segue:

• per ogni indice di valutazione della probabilità i (i=1…6) calcolare il valore P_i ;
• per ogni indice di valutazione dell’impatto j (j=1…4) calcolare il valore I_j ;
• calcolare le medie P_m e I_m ;
• calcolare il prodotto R=P_m ^. I_m .

Analizzando alcuni dei dati pubblicati dalle Pubbliche Amministrazioni, in particolare quelle della PA centrale, in questi primi anni di attuazione del PNA, si evince che l’applicazione del procedimento sopra indicato nel PNA 2013 porta, tipicamente, ad un istogramma dei valori di rischio che assume in linea di massima una forma simile a quella riportata a titolo di esempio in fig.3.

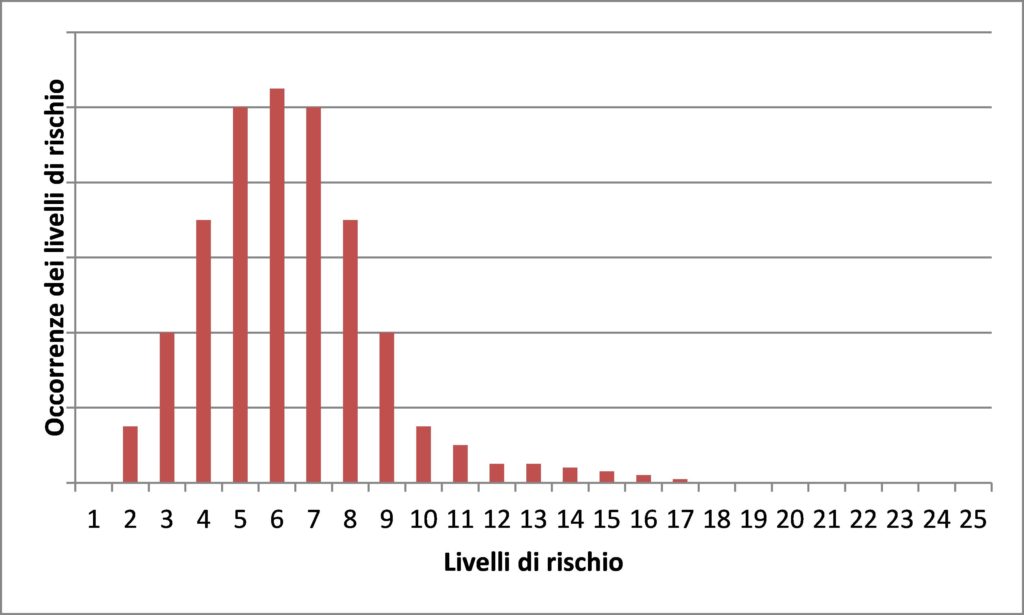
L’istogramma rappresenta, per ogni singolo valore del livello di rischio (da 0, 1, 2 fino a 25, valori delle ascisse) il numero di occorrenze verificate nel campione considerato. In fig.3 non sono riportati i valori in ordinata, in quanto il diagramma è qui riportato solo per fornire una informazione qualitativa, ma è tuttavia rappresentativo delle risultanze ottenute dalla stragrande maggioranza delle Amministrazioni che hanno applicato alla lettera il metodo proposto nel PNA 2013 per l’analisi del rischio.

Dall’osservazione della fig.3 possiamo rilevare che:

1. i livelli di rischio sono praticamente tutti concentrati nella parte bassa (prima metà) dell’intervallo potenzialmente occupabile (teoricamente da 0 a 25);
2. nella seconda metà dell’intervallo (da 16 a 25) si registra, nella pratica, l’assenza di occorrenze dei valori di rischio;
3. la media dei livelli di rischio si posiziona al centro della prima decade, con valori tipicamente bassi (tra 4 e 7) rispetto al range di possibile variazione del livello di rischio teorico.

In sintesi, l’indicazione fornita in [7] sull’utilizzo dell’operatore di media proposto nel 2013 presenta una criticità perché tende a orientare verso il basso i livelli di rischio valutato, non rendendo utile lo sviluppo sull’intera dinamica dei livelli e rischiando di mascherare eventuali valori estremi di impatto o probabilità.

La principale ragione di questo fenomeno risiede nella scelta della media aritmetica per caratterizzare il comportamento delle variabili impatto e probabilità. La scelta di questo indicatore può condurre ad una sottostima del rischio e induce, per questo, ad un appiattimento verso il basso. In altri termini, l’appiattimento è una conseguenza della sottostima sistematica che l’indicatore ‘media aritmetica’ produce.

Volendo esemplificare la problematica in modo tangibile, si può pensare ad una catena in cui ogni singolo anello rappresenti uno dei diversi indicatori di probabilità (o impatto). Volendo calcolare la resistenza della catena ad una forza di trazione, non sarà rilevante conoscere la resistenza media degli anelli, ma la resistenza dell’anello più debole, perché sarà proprio quello che si spezzerà per primo.

Analogamente, per valutare il rischio di riuscita di un attacco corruttivo, non sarà tanto rilevante la robustezza media di fronte ai vari possibili attacchi (probabilità) ma solo individuare le componenti con valore più alto, perché verosimilmente, su di esse si concentrerà l’attacco.

Per fare un esempio numerico reale, consideriamo un processo P_A caratterizzato dalle sei componenti di probabilità P_A={1,2,5,1,1,2}. Il valore medio di probabilità è in questo caso uguale a 2, così come sarà uguale a 2 nel caso di un secondo processo P_B caratterizzato, per esempio, dalle sei componenti P_B={2,2,3,3,1,1}. E’ evidente però che i due processi presentano, dall’osservazione delle singole componenti, caratteristiche di robustezza significativamente diverse, che dovranno condurre all’implementazione di misure differenti. Mediante l’utilizzo della probabilità media, la criticità in P_A legata al terzo indice di valutazione con livello di probabilità pari a 5 viene completamente trascurata.

Analoghe considerazioni si possono condurre con riferimento agli indici di impatto.

Confronto tra diversi operatori statistici per il calcolo del livello di rischio

Per rappresentare il diverso comportamento di distinti operatori statistici utilizzabili nella definizione del livello di rischio per il caso in esame, in fig.4 sono riportati i risultati ottenuti per 13 processi lavorativi distinti analizzati dagli autori, su cui si sono applicate tre diverse metodologie di calcolo del rischio corruttivo, agendo sui diversi valori di P e I ottenuti per i diversi indici e per ciascun processo. Le tre metodologie sono legate in questa breve analisi agli operatori di: media, valore massimo e media corretta.

In particolare:

1. per il caso della media (caso già descritto concettualmente in precedenza) il livello di rischio medio R_med si calcola, avendo indicato i valori medi della probabilità e dell’impatto come P_med e I_med , attraverso la relazione
   (1) R_med = P_med ^. I_med ,
2. per il caso del valore massimo il livello di rischio massimo R_MAX si calcola, avendo indicato i valori massimi della probabilità e dell’impatto – derivanti dalle risposte ai diversi quesiti che caratterizzano gli indicatori – come P_MAX e I_MAX , attraverso la relazione
   (2) R_MAX = P_MAX ^. I_MAX ,
3. per il caso della media corretta, indicheremo invece con P_mc e con I_mc rispettivamente la probabilità e l’impatto medio corretto calcolato con le relazioni qui di seguito riportate
   (3) P_mc = P_med +^.σ(P) se P_mc ≤5, altrimenti P_mc = 5
   (4) I_mc = I_med +^.σ(I) se I_mc ≤5 , altrimenti I_mc = 5

dove:

• P_med è il valore medio ottenuto per la probabilità;
• I_med è il valore medio ottenuto per l’impatto;
• σ è l’operatore di deviazione standard;
• l’operazione di troncamento al valore massimo 5 si rende necessaria per contenere entro le scale prefissate i valori di P, I

e per il Rischio medio corretto indicato con R_mc utilizzeremo, infine, la relazione

(5) R_mc = P_mc ^. I_mc .

Lo scopo di questa comparazione è determinare gli eventuali punti di forza e di debolezze di diversi metodi al fine di poter superare le criticità dell’operatore media aritmetica consigliato in prima istanza dal normatore nel 2013.

La sintesi dei risultati numerici ottenuta per i 13 processi analizzati è riportata in Tab.2, mentre in Fig.4 si mostrano graficamente gli stessi risultati per facilitare l’evidenziazione delle principali caratteristiche.

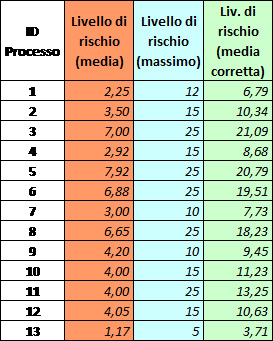
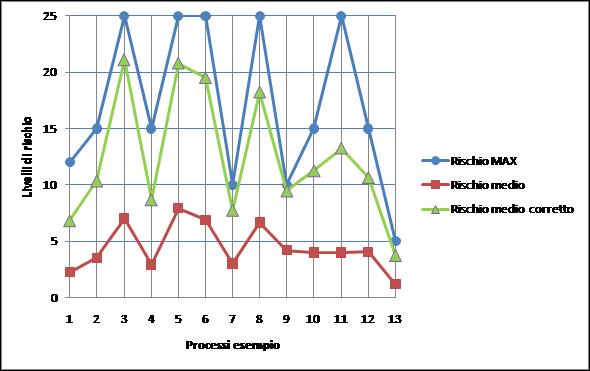
L’osservazione dei risultati di fig.4 consente di affermare che:

1. il metodo legato alla media, come già anticipato, schiaccia fortemente la dinamica del livello rischio su valori medio bassi, non consentendo di determinare con precisione – anche dopo una eventuale normalizzazione – una classifica coerente e affidabile dei processi più a rischio;
2. a parità di dati in ingresso i metodi legati al massimo e alla media corretta consentono di caratterizzare con più dettaglio rispetto al metodo della media i processi critici, sfruttando tutta la dinamica disponibile per R, da 0 a 25;
3. il metodo legato alla valore massimo, pur evidenziando meglio i processi critici rispetto al caso della media, presenta le seguenti principali debolezze:
   • non tiene in nessun conto dell’ampiezza di tutti gli altri valori componenti esclusi. Per esempio se il valore di P è determinato dalle sue sei componenti {1,1,5,1,1,2} il valore massimo sarà 5 così come sarà uguale a 5 nel caso P determinato dalle sei componenti {4,5,5,4,5,4}, ma è evidente che i due processi in sé non presentano la stessa robustezza complessiva;
   • una valutazione errata in senso peggiorativo di uno solo dei valori componenti P e I potrebbe falsare pesantemente la stima del livello di rischio, conducendo ad una sovrastima eccessiva del valore;
4. il metodo della media corretta consente di:
   • ridurre gli effetti di sottostima sottostanti alla scelta del metodo della media aritmetica;
   • assicurare un peso effettivo ad ogni singolo valore componente di P e di I attraverso l’utilizzo sia della media sia della deviazione standard;
   • ridurre gli effetti di sovrastima sottostanti alla scelta del metodo legato al valore massimo;
   • di attenuare l’influenza di eventuali errori di valutazione sulle singole componenti;
   • di distinguere con una buona precisione tra loro i livelli di rischio, facilitando l’individuazione dei processi più a rischio e la creazione di classifiche affidabili.

Alla luce di quanto osservato possiamo affermare che, a parità di processo e di valori di partenza di probabilità e impatto, la scelta del metodo di combinazione dei valori numerici degli indici di valutazione determina un livello rischio completamente diverso per ampiezza della misura e significativamente diverso come classifica di rischio finale. Un’accurata analisi statistica della vasta mole di dati oggi disponibili nella PA potrebbe guidare alla scelta di metodi di calcolo che, con l’utilizzo di opportune pesature statistiche, possano tenere nel giusto conto tutti gli aspetti utili per una corretta valutazione dei rischi per la prevenzione della corruzione.

Glossario

• DFP Dipartimento della Funzione Pubblica – PCM
• ISO International Standard Institute
• PA Pubblica Amministrazione
• PCM Presidenza del Consiglio dei Ministri
• PDCA Plan Do Check Act – ciclo di Deming
• PNA Piano Nazionale Anticorruzione

Bibliografia e sitografia

• [1] Legge 190 del 6 novembre 2012, Disposizioni per la prevenzione e la repressione della corruzione e dell’illegalità nella pubblica amministrazione.
• [2] PCM-DFP, Piano Nazionale Anticorruzione, Corpo Principale del Piano, 2013
• [3] ISO31000: Risk management — Principles and guidelines, 2009.
• [4] ISO31010: Risk assessment techniques, 2009.
• [5] P. Senni, La filosofia di Deming e il ciclo PDCA, AICQ
• [6] PCM-DFP, Piano Nazionale Anticorruzione, Allegato 5 – Valutazione del livello di Rischio, 2013
• [7] PCM-DFP, Addendum Allegato 5 PNA – Algoritmo calcolo impatto e probabilità, 2013
• [8] PCM-DFP, Piano Nazionale Anticorruzione, Allegato 1 – Soggetti, azioni e misure finalizzati alla prevenzione della corruzione, 2013

 

A cura di: Marco Carbonelli, Laura Gratta, Michele de Nittis