Modello analitico per l’analisi dei rischi

Le organizzazioni vivono una situazione molto dinamica e dove la sicurezza della sopravvivenza non viene sempre garantita. L’analisi dei rischi aziendali è quindi diventata una metodologia preventiva, in tutti settori, per il mantenimento ed il miglioramento delle aziende. Il Risk Management è allora un’attività prioritaria ed imprescindibile.

L’analisi dei rischi viene poi richiesta in particolar modo per la tutela dei dati e in tale ottica e su precise indicazioni legislative (Dlgs 196/03) e normative (ISo 27001 e ISo 3100), cercheremo di sviluppare un modello che permetta una analisi dei rischi quantitativa e qualitativa nella definizione dei parametri.

I rischi dei dati sono generalmente funzione di due variabili: la probabilità che questo accada e la gravità del fenomeno.

Possiamo allora individuare l’indicatore i – esimo dei rischi come:

Ri = f(φi, Υi)

con φi la probabilità dell’evento e Υi la sua gravità.

L’indicatore rischio globale risulta essere:

R = Σi Ri

Possiamo dare una definizione di Probabilità e Gravità come segue:

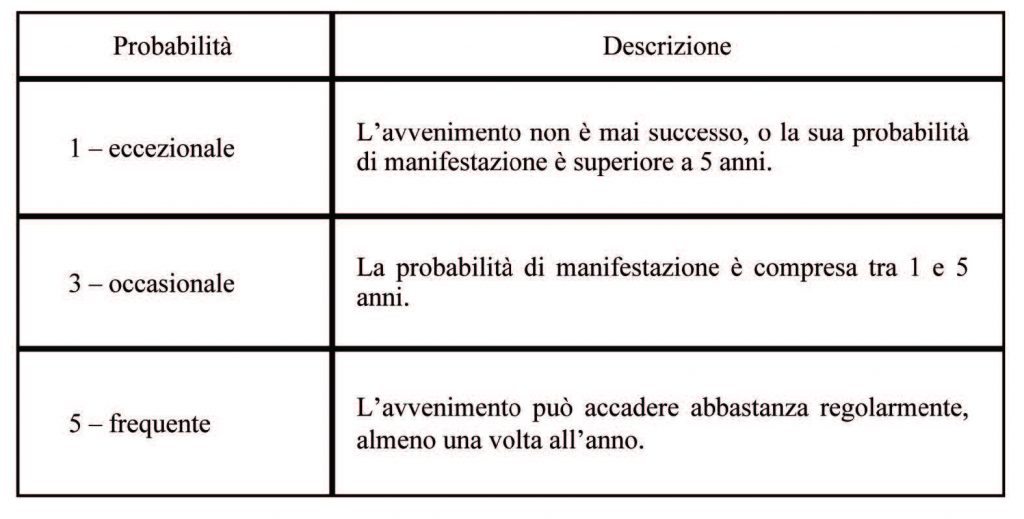
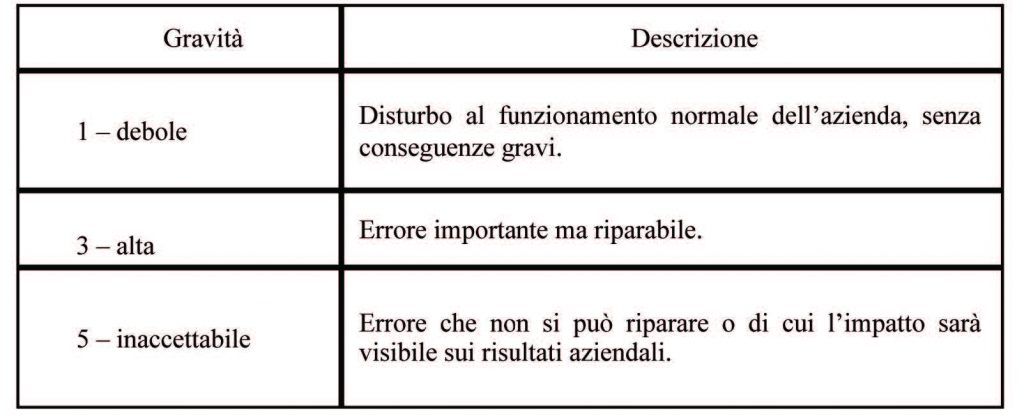
La tabella seguente riporta la matrice Gravità e Probabilità

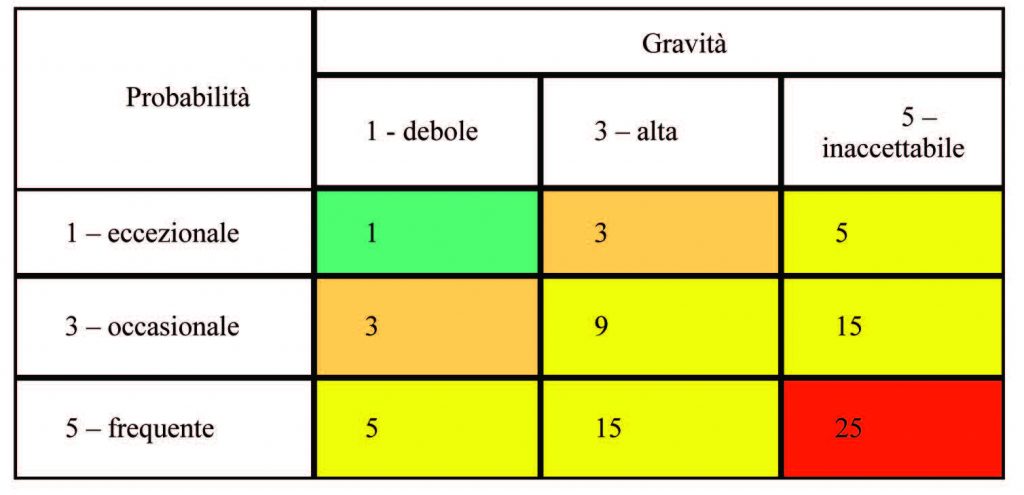
La gravità però è, a sua volta, influenzata da due fattori: l’impatto economico ed il tempo di ripristino. Cioè quanto grande risulta l’impatto del danno avvenuto e quando tempo è necessario per riportare il sistema nelle condizioni iniziali.

Quindi, con e l’indicatore dell’impatto economico e t il tempo di ripristino,

Υi = f(ei, ti)

Allora si può scrivere:

Ri = f(φi, Υi) = f(φi, ei, ti,)

Riassumendo nella tabella seguente:

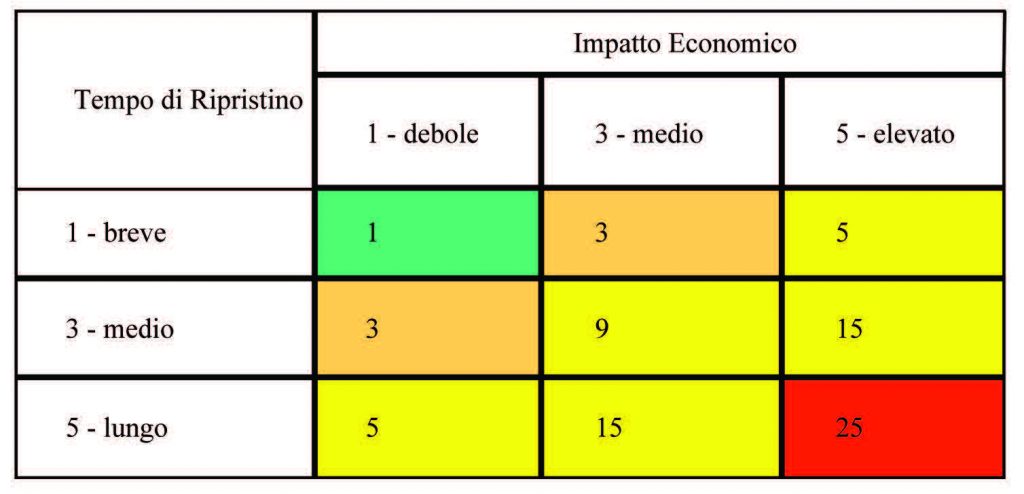
Se consideriamo la gravità come prodotto dell’impatto economico e del tempo di ripristino otteniamo:

Υi = ei*ti (5)

Il calcolo del rischio, può essere ricondotto al prodotto tra la probabilità e la gravità:

Ri = φi*Υi = φi*ei* ti

Introduciamo ora altre variabili che sono:

χi = risulta essere la posizione dei dati (in locale, cloud, conservata in server farm, etc) che può assumere valori discreti 1;3;5 a seconda se il dato è facilmente rintracciabile (valore 1) o se è invece è conservato ad esempio in cloud o irrintracciabile (valore 5);

ηi = è il numero di dati trattati, anche questo assume valori discreti 1;3;5 a seconda della quantità, ad esempio può valere 1 se abbiamo un numero di dati < di 1000, 3 se sono < di 10000 o 5 se sono > di 10000;

τi = è il numero di trattamenti a cui sono sottoposti i dati, anche in questo caso assume valori discreti 1;3;5 a seconda dei trattamenti 1 se i trattamenti sono solo > 1; 3 se sono > 5 e 5 se sono > 10;

ςi = è il numero dei controlli sulle misure di sicurezza dei dati, maggiori sono i controlli e minori risulteranno i rischi.

ςi risulta allora essere una funzione delle variabili sopra riportate:

ςi = f(χi, ηi, τi,) dove risulta ςi = (1/χi* 1/ηi* 1/τi)

a questo punto allora i rischi possono essere descritti come:

Ri = φi*Υi = φi*ei* ti*(1/ςi)

Ma così fatta l’analisi dei rischi risulta ancora non completa, è necessario introdurre un’altra variabile, la variabile misure di sicurezza.

Questa è formata dal prodotto di tre sotto misure: sicurezza fisica (σ1), sicurezza logica (σ2) e sicurezza organizzativa (σ3).

σ i = (σ1* σ2* σ3)

Anche in questo caso le sicurezze assumono i valori 1; 3 e 5 a seconda della loro implementazione (5 sicurezza massima o completa).

Quindi i rischi risultano allora così formulati:

Ri = φi*ei* ti*[1/(1/χi* 1/ηi* 1/τi)]*1/ σ i = φi*ei* ti*[1/(1/χi* 1/ηi* 1/τi)]*1/ (σ1* σ2* σ3)

Ora tutte le grandezze individuate possono assumere i valori discreti 1,3 e 5.

Calcoliamo allora alcun esempi dei rischi come riportato nella tabella seguente:

Dalla tabella si nota come i valori, in riferimento all’algoritmo sopra indicato, seguano tutti la stessa regola, questo supporta il modello presentato.

Graficando i dati relativi ai rischi ed ai controlli otteniamo:

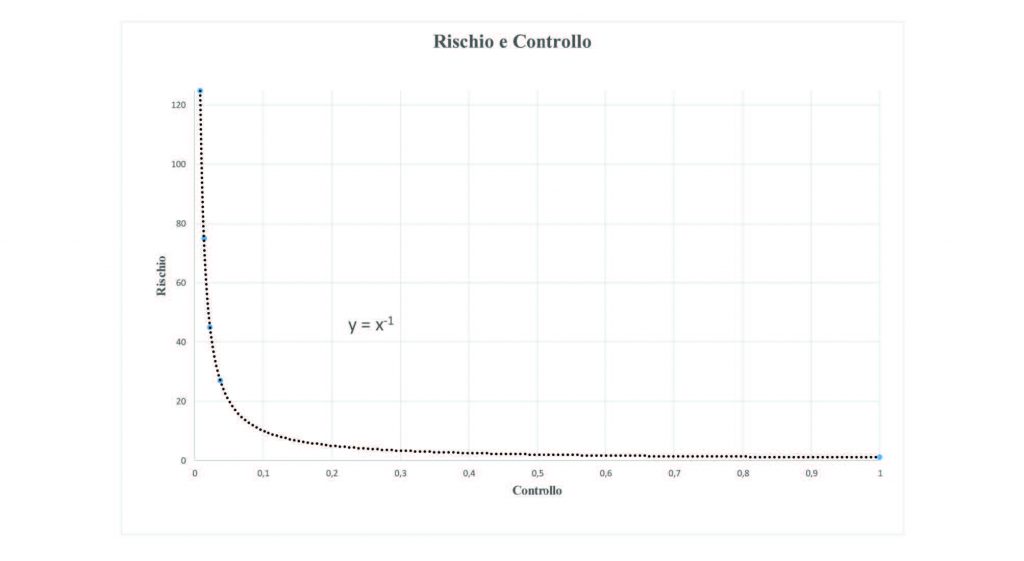
La curva ottenuta risulta un’iperbole di equazione y = x-1, questa risulta valida per tutte le combinazioni dei parametri individuati sopra.

Dal risultato dell’algoritmo risulta allora abbastanza semplice collocare i vari rischi sulla curva in modo da avere una visione immediata della situazione. Tale procedura deve essere iterata per tutti i rischi individuati. Ad esempio per ogni dB o cluster di dati presenti in azienda.

Il rischio aziendale risulterà la sommatoria di tutti i singoli rischi:

R = Σi Ri

Per poter individuare correttamente i parametri ed eseguire i calcoli sopra citati è necessario effettuare un preciso assessment sui dati utilizzati in azienda ed il loro flusso, un supporto può essere fornito sia dalle normative in vigore (ISo 31000, ISo 27001, etc) che da una precisa analisi di processo.

L’analisi e la gestione dei rischi aziendali è, e deve essere, patrimonio delle organizzazioni a tutti i livelli. Viene descritta una metodologia sistemica per la valutazione dei rischi. Tale valutazione utilizza più variabili collegate tra di loro che permettono di avere una visione globale dei dati. I dati devono quindi essere raccolti e gestiti in modo corretto considerando il Risk Management come un processo strategico dell’azienda.

SOLO UNA CORRETTA ANALISI PERMETTE DI INDIVIDUARE I RISCHI E MITIGARLI, È NECESSARIO AVERE UNA VISIONE COMPLETA DEI RISCHI E DELLE SICUREZZA A CUI I NOSTRI DATI SONO TRATTATI, QUESTO COMPORTA UN’ANALISI CORRETTA ANCHE DELLE VULNERABILITÀ

 

A cura di: Stefano Gorla, Privacy Business Unit Director – Digital Preservation Officer Consultant Seen Solution SRL e delegato regionale Lombardia Andip